2. Compute travel times

This notebook computes the travel times from all the points of a three-dimensional grid to each seismic station. These travel times are necessary for time-shifting the seismic traces when evaluating the beamformed network response at every location of the grid.

This tutorial utilizes the pykonal package to compute travel times given a velocity model. The package documentation and installation procedure are described in the pykonal package documentation. Please acknowledge White et al. (2020) if using pykonal.

Note: although pykonal handles computing the travel times in a three-dimensional velocity model, the example below uses a one-dimensional velocity model.

Contents

• Read velocity model

• Interpolate velocity model at depth

• Expand model laterally

• Get station coordinates

• Show model and stations

• Compute travel times

• Save travel times

• Show travel times at a given station

import h5py as h5
import numpy as np
import os
import pandas as pd
import tqdm

from matplotlib import pyplot as plt

from obspy import read, read_inventory
from pykonal.solver import PointSourceSolver
from pykonal.transformations import geo2sph

Read velocity model

We wrote the velocity model of Karabulut et al. (2011) in a csv file that we read with pandas. The model is given in meters for the depth and in m/s for the speed values. Everything is converted to km for compatibility with pykonal.

FILEPATH_VELOCITY = "../data/velocity_model_Karabulut2011.csv"

# Read velocity model
velocity_layers = pd.read_csv(
    FILEPATH_VELOCITY,
    usecols=[1, 2, 4],
    names=["depth", "P", "S"],
    skiprows=1,
    index_col="depth",
    )

# Convert meters to kilometers
velocity_layers *= 1e-3
velocity_layers.index *= 1e-3

# Show table
velocity_layers.T

depth	-2.0	0.0	1.0	2.0	3.0	4.0	5.0	6.0	8.0	10.0	12.0	14.0	15.0	20.0	22.0	25.0	32.0	77.0
P	2.90	3.0	5.60	5.70	5.80	5.90	5.95	6.05	6.10	6.15	6.20	6.25	6.30	6.40	6.50	6.70	8.00	8.045
S	1.67	1.9	3.15	3.21	3.26	3.41	3.42	3.44	3.48	3.56	3.59	3.61	3.63	3.66	3.78	3.85	4.65	4.650

ax = velocity_layers.plot(
    drawstyle="steps-post",
    ylabel="Wave Velocity (km/s)",
    xlabel="Depth (km)",
    title="1D velocity model from Karabulut et al. 2011",
    grid=True,
)

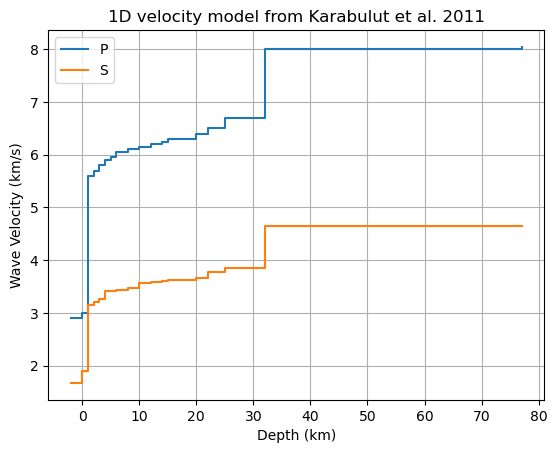
Interpolate velocity model at depth

We compute the travel times on a finer grid than the model grid, so we need to interpolate the model. We define 30 depths between 30 km and -2 km.

depths = np.linspace(30.0, -2.0, 32)

Then we interpolate the velocity at the given depths using pandas.DataFrame method reindex.

velocity_layers_interp = velocity_layers.reindex(depths, method="ffill")

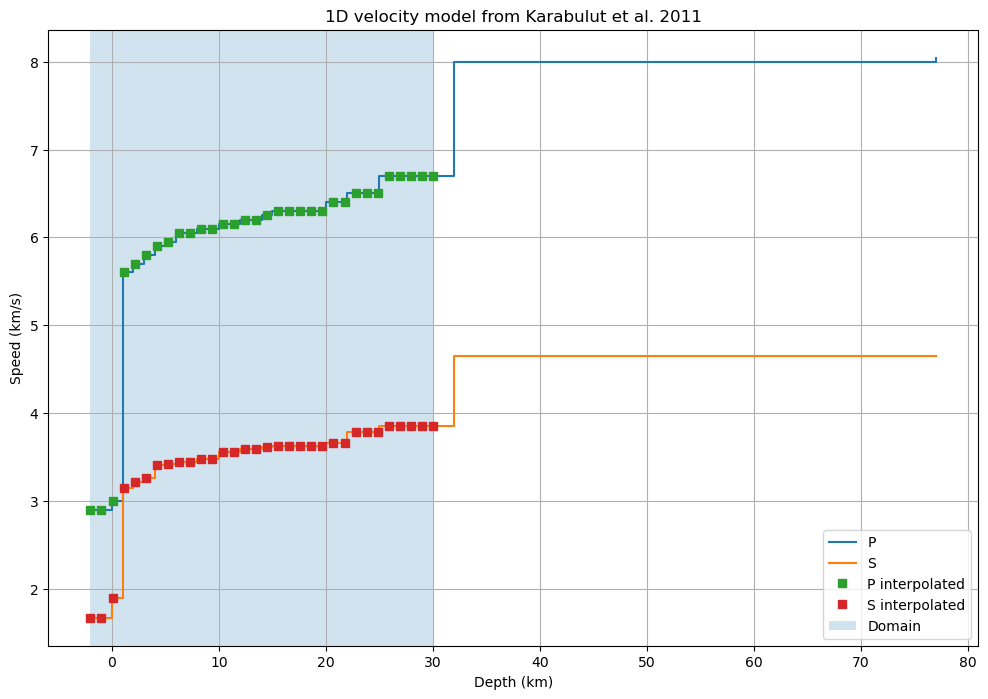
We can then compare the natural (layered) and interpolated models as a function of depth

velocity_layers.plot(drawstyle="steps-post")
velocity_layers_interp.sort_values("depth").plot(
    drawstyle="steps-post",
    xlabel="Depth (km)",
    ylabel="Speed (km/s)",
    title="1D velocity model from Karabulut et al. 2011",
    ax=plt.gca(),
    grid=True,
    figsize=(12, 8),
    marker="s",
    ls=""
)

# Labels and legends
plt.axvspan(depths.min(), depths.max(), alpha=0.2)
plt.legend(["P", "S", "P interpolated", "S interpolated", "Domain"])
plt.show()

Expand model laterally

Because pykonal uses three-dimensional coordinate systems, we need to cast the one-dimensional velocity model onto a three-dimensional grid. The following define the grid in the longitude and latitude dimensions.

velocity_layers_interp

	P	S
depth
30.000000	6.70	3.85
28.967742	6.70	3.85
27.935484	6.70	3.85
26.903226	6.70	3.85
25.870968	6.70	3.85
24.838710	6.50	3.78
23.806452	6.50	3.78
22.774194	6.50	3.78
21.741935	6.40	3.66
20.709677	6.40	3.66
19.677419	6.30	3.63
18.645161	6.30	3.63
17.612903	6.30	3.63
16.580645	6.30	3.63
15.548387	6.30	3.63
14.516129	6.25	3.61
13.483871	6.20	3.59
12.451613	6.20	3.59
11.419355	6.15	3.56
10.387097	6.15	3.56
9.354839	6.10	3.48
8.322581	6.10	3.48
7.290323	6.05	3.44
6.258065	6.05	3.44
5.225806	5.95	3.42
4.193548	5.90	3.41
3.161290	5.80	3.26
2.129032	5.70	3.21
1.096774	5.60	3.15
0.064516	3.00	1.90
-0.967742	2.90	1.67
-2.000000	2.90	1.67

longitudes = np.linspace(30.20, 30.45, 25)
# sample latitudes in decreasing order to get corresponding colatitudes in increasing order (see explanation further)
latitudes = np.linspace(40.76, 40.60, 16)

We then expand the velocity vector in the longitude and latitude dimensions with xarray. This operation is automatically done with the expand_dim() method.

velocity_P = np.zeros((len(depths), len(latitudes), len(longitudes)), dtype=np.float32)
velocity_S = np.zeros((len(depths), len(latitudes), len(longitudes)), dtype=np.float32)
# use numpy's broadcasting rules
velocity_P[...] = velocity_layers_interp["P"].values[:, None, None]
velocity_S[...] = velocity_layers_interp["S"].values[:, None, None]
# store the P- and S-wave velocity models in a dictionary
velocity_model = {
    "P": velocity_P,
    "S": velocity_S
}

Station coordinates

We extract the station coordinates from the XML files.

# Get inventories
inventory = read_inventory("../data/processed/*xml")

# Extract stations
stations = [sta for net in inventory for sta in net]
attrs = "longitude", "latitude", "elevation", "code"
stations = [{item: getattr(sta, item) for item in attrs} for sta in stations]

# Turn into dataframe
network = pd.DataFrame(stations).set_index("code")
network["depth"] = -1e-3 * network.elevation

# Save network metadata
network.to_csv("../data/network.csv")

# Show
network

	longitude	latitude	elevation	depth
code
DC06	30.265751	40.616718	555.0	-0.555
DC07	30.242170	40.667080	164.0	-0.164
DC08	30.250130	40.744438	162.0	-0.162
DD06	30.317770	40.623539	182.0	-0.182
DE07	30.411539	40.679661	40.0	-0.040
DE08	30.406469	40.748562	31.0	-0.031
SAUV	30.327200	40.740200	170.0	-0.170
SPNC	30.308300	40.686001	190.0	-0.190

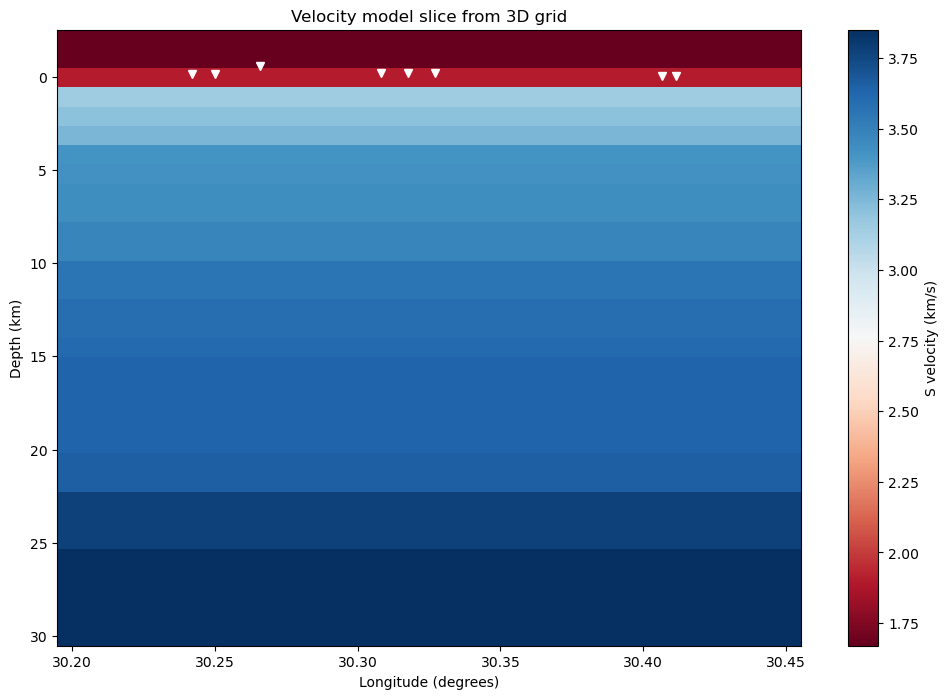
Show model and stations

This cell selects a slice of the velocity model with the DataArray.sel() and plots it.

# Select slice at first latitude index
phase = "S"
velocities_slice = velocity_model[phase][:, 0, :]

# Show velocities
fig = plt.figure(figsize=(12, 8))
img = plt.pcolormesh(longitudes, depths, velocities_slice, cmap="RdBu")
cb = plt.colorbar(img)

# Show stations
plt.plot(network.longitude, network.depth, "wv")

# Labels
ax = plt.gca()
ax.set_xlabel("Longitude (degrees)")
ax.set_ylabel("Depth (km)")
ax.set_title("Velocity model slice from 3D grid")
cb.set_label(f"{phase} velocity (km/s)")
ax.invert_yaxis()

Compute travel times

The travel times are computed for every station with the Eikonal solver of pykonal. The travel times are then saved into a h5 file for later use.

Warning: For pykonal, we need to give the velocity grid in spherical coordinates \((r, \theta, \varphi)\), which is why we built the grid with decreasing depths and latitudes.

Spherical coordinates: - \(r\): Distance from center or Earth in km (= decreasing depth). - \(\theta\): Polar angle in radians (= co-latitude or, equivalently, decreasing latitude). - \(\varphi\): Azimuthal angle in radians (= longitude).

STATION_ENTRIES = ["latitude", "longitude", "depth"]

# Initialize travel times
travel_times = {}

# Reference point
reference_point = geo2sph((latitudes.max(), longitudes.min(), depths.max()))
node_intervals = (
    np.abs(depths[1] - depths[0]),
    np.deg2rad(np.abs(latitudes[1] - latitudes[0])),
    np.deg2rad(longitudes[1] - longitudes[0]),
)

# Loop over stations and phases
for phase in velocity_model:
    travel_times[phase] = {}
    for station in tqdm.tqdm(network.index, desc=f"Travel times {phase}"):

        # Initialize Eikonal solver
        solver = PointSourceSolver(coord_sys="spherical")
        solver.velocity.min_coords = reference_point
        solver.velocity.node_intervals = node_intervals
        velocity = velocity_model[phase]
        solver.velocity.npts = velocity.shape
        solver.velocity.values = velocity.copy()

        # Source
        src_loc = network.loc[station][STATION_ENTRIES].values
        solver.src_loc = np.array(geo2sph(src_loc).squeeze())

        # Solve Eikonal equation
        solver.solve()

        # Update the travel_times dictionary
        tt = solver.tt.values
        # pykonal might produce a singularity at origin
        tt[np.isinf(tt)] = 0
        travel_times[phase][station] = tt

Travel times P:   0%|          | 0/8 [00:00<?, ?it/s]

Travel times P: 100%|██████████| 8/8 [00:03<00:00,  2.01it/s]
Travel times S: 100%|██████████| 8/8 [00:03<00:00,  2.08it/s]

Save travel times and grid coordinates

Save the travel times as a hdf5 file. This format preserves a self-explanatory data structure and supports compression.

# build 3D gridded coordinates from depths, latitudes and longitudes vectors
# these are the coordinates of the points in the travel time grid
depths_g, latitudes_g, longitudes_g = np.meshgrid(
    depths, latitudes, longitudes, indexing="ij"
)

with h5.File("../data/travel_times.h5", mode="w") as ftt:
    ftt.create_group("source_coordinates")
    ftt["source_coordinates"].create_dataset("depth", data=depths_g)
    ftt["source_coordinates"].create_dataset("latitude", data=latitudes_g)
    ftt["source_coordinates"].create_dataset("longitude", data=longitudes_g)
    for phase in ["P", "S"]:
        ftt.create_group(phase)
        for sta in travel_times[phase]:
            ftt[phase].create_dataset(sta, data=travel_times[phase][sta])

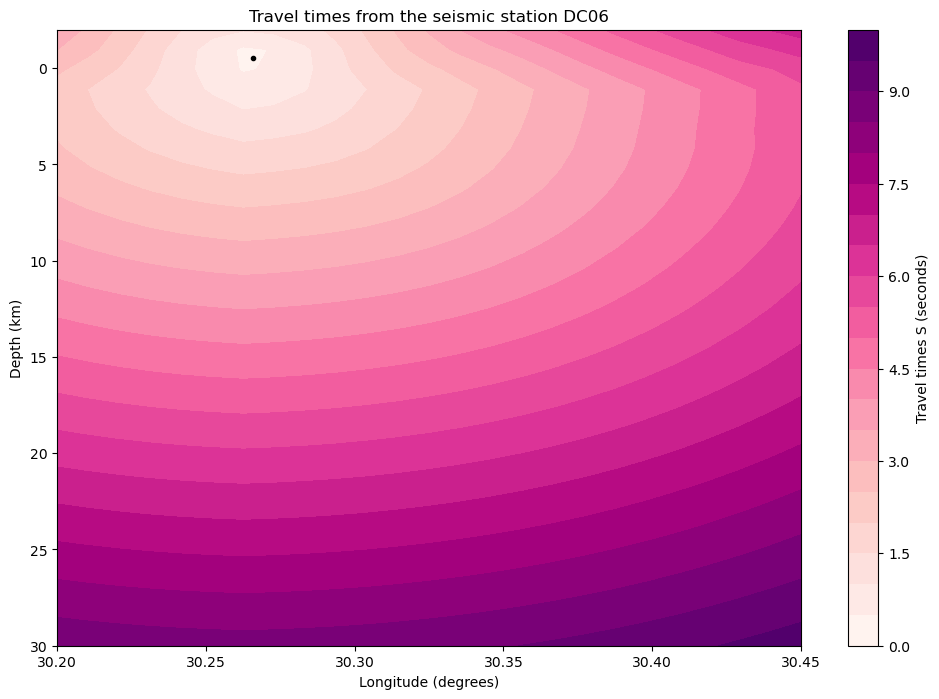
Show travel times at a given station

CONTOUR_LEVELS = 20
SEISMIC_PHASE = "S"
station = network.loc["DC06"]

# Show
latitude_id = np.abs(latitudes - station.latitude).argmin()
time_delays = travel_times[SEISMIC_PHASE][station.name]
time_delays = time_delays[:, latitude_id, :]
fig = plt.figure(figsize=(12, 8))
img = plt.contourf(longitudes, depths, time_delays, cmap="RdPu", levels=CONTOUR_LEVELS)

# Colorbar
cb = plt.colorbar(img)
cb.set_label(f"Travel times {SEISMIC_PHASE} (seconds)")

# Station
plt.plot(station.longitude, station.depth, "k.")

# Labels
ax = plt.gca()
ax.invert_yaxis()
ax.set_xlabel("Longitude (degrees)")
ax.set_ylabel("Depth (km)")
ax.set_title(f"Travel times from the seismic station {station.name}")
plt.show()